Brief Summary
This video demonstrates the algebraic identity (a + b)² = a² + 2ab + b² using a visual, working model made from cardboard. The model breaks down a larger square with side length (a + b) into smaller squares and rectangles, illustrating how their combined areas equal the area of the original square.
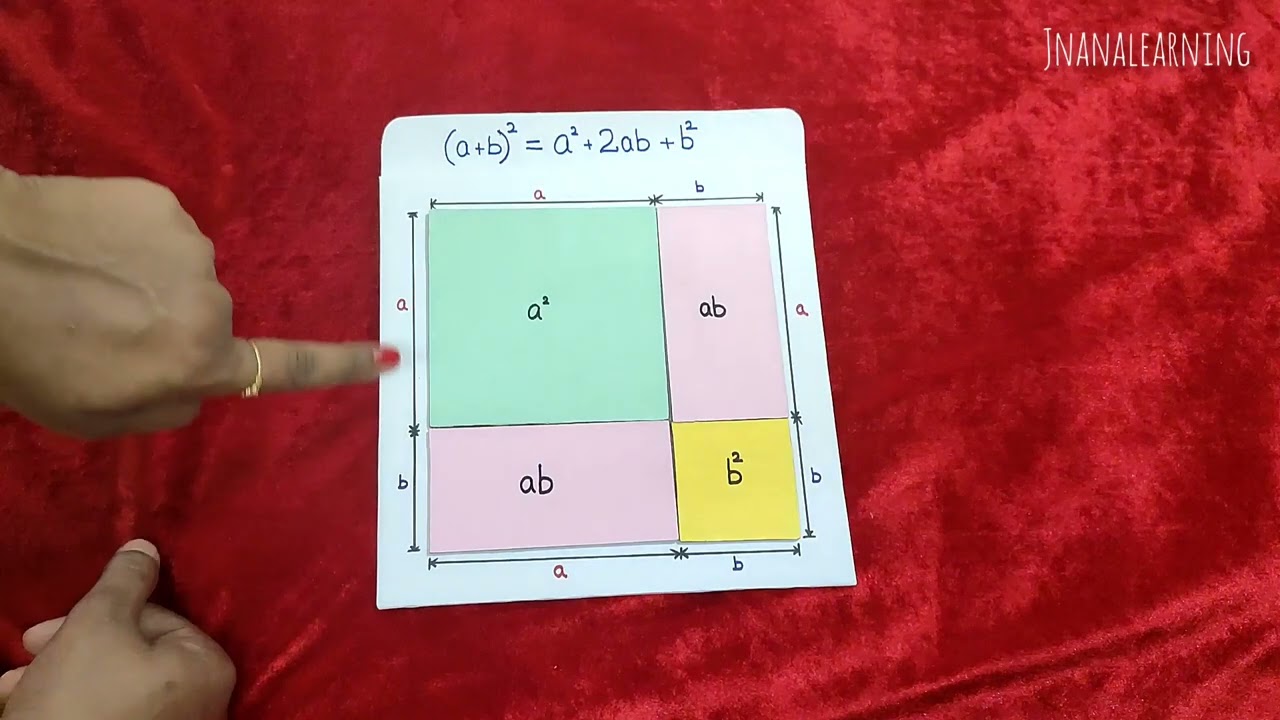
- The model uses a square with side (a + b) to represent (a + b)².
- It decomposes this square into a square of area a², two rectangles of area ab, and a square of area b².
- This visual representation helps to understand and remember the algebraic identity.
Introduction
The video introduces a working model to visually prove the algebraic identity (a + b)² = a² + 2ab + b². This identity is a fundamental concept in algebra, and the model aims to provide a clear and intuitive understanding of it.
Building the Model
The presenter starts with a square that has sides of length (a + b), so the area of the whole square is (a + b)². A square piece with side 'a' is placed on the big square, representing an area of a². Then, a rectangular piece with length 'a' and width 'b' is placed next to the square, representing an area of ab. Another identical rectangular piece is placed adjacent to the first one, also representing an area of ab. Finally, a smaller square piece with side 'b' is placed to fill the remaining space, representing an area of b².
Proving the Identity
By assembling the pieces, it's shown that the large square with area (a + b)² is composed of a square with area a², two rectangles each with area ab, and a square with area b². This visually demonstrates that (a + b)² = a² + ab + ab + b², which simplifies to (a + b)² = a² + 2ab + b². The presenter emphasises that the total area of the large square is equal to the sum of the areas of the four smaller pieces.
Creating Your Own Model
The video suggests that viewers can easily create this working model themselves using cardboard pieces. By cutting a square piece and dividing it accordingly, then placing the square and rectangular pieces in the correct order, anyone can prove this algebraic identity.