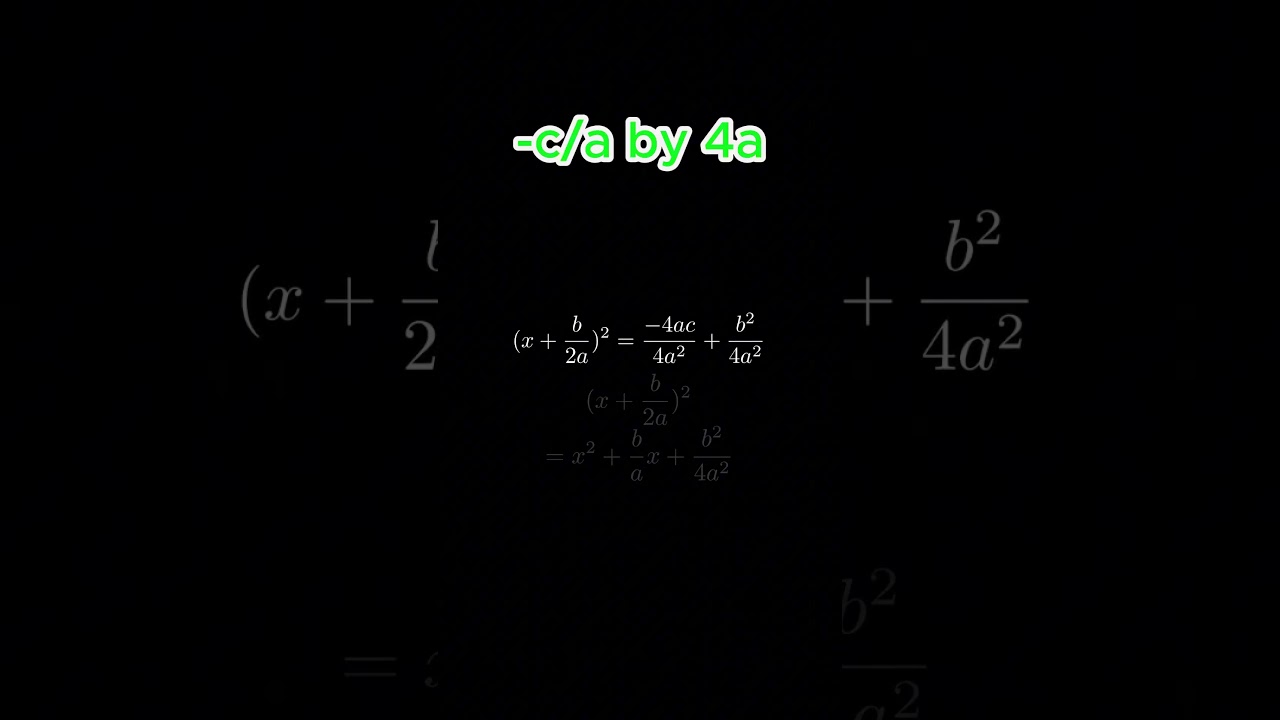Brief Summary
This video explains the derivation of the quadratic formula. It starts by manipulating the standard quadratic equation through algebraic steps such as subtracting C, dividing by A, completing the square, and taking square roots. The derivation logically progresses to isolate x, ultimately revealing the well-known quadratic formula.
- Starts with standard quadratic equation
- Uses algebraic steps to isolate x
- Derives the quadratic formula
Introduction
The video introduces the quadratic formula, a fundamental concept in algebra, setting the stage for a detailed explanation of its derivation. The presenter aims to demystify the formula by showing the step-by-step process of how it is obtained from a standard quadratic equation.
Deriving the Quadratic Formula: Initial Steps
The derivation begins by manipulating the standard quadratic equation. First, C is subtracted from both sides of the equation, and then both sides are divided by A. This sets up the equation for completing the square, a crucial step in isolating x.
Completing the Square
The video then focuses on completing the square. The expression X + B over 2A squared is introduced, which expands to X^2 + BAX + B^2 over 4A^2. Adding B^2 over 4A^2 to both sides of the equation allows the left side to be expressed as a perfect square, simplifying the equation.
Simplifying and Combining Terms
After completing the square, the equation is further simplified. The left side is replaced with the squared expression, and the right side is manipulated to combine terms. Multiplying the top and bottom of the C/A term by 4A allows for the combination of the terms on the right side into a single fraction.
Isolating x: Taking Square Roots
To isolate x, the square root of both sides of the equation is taken. It's important to remember the plus and minus sign on the right side when taking the square root. The square root is applied to both the numerator and the denominator of the fraction, and the square root of 4A^2 simplifies to 2A.
Final Steps: Quadratic Formula
The final steps involve isolating x completely. B over 2A is subtracted from both sides of the equation. This results in combining the terms on the right side, leading to the final form of the quadratic formula.
Conclusion
The video concludes by highlighting the derived quadratic formula. The presenter encourages viewers to like and subscribe to the channel if they found the explanation helpful.