Brief Summary
This video explains quantum numbers and how they determine the arrangement of electrons in an atom. It covers the four quantum numbers (principal, angular momentum, magnetic, and spin), their significance, and how they relate to atomic orbitals. The video also discusses the Aufbau principle, Hund's rule, electron configurations, orbital diagrams, and the magnetic properties of atoms.
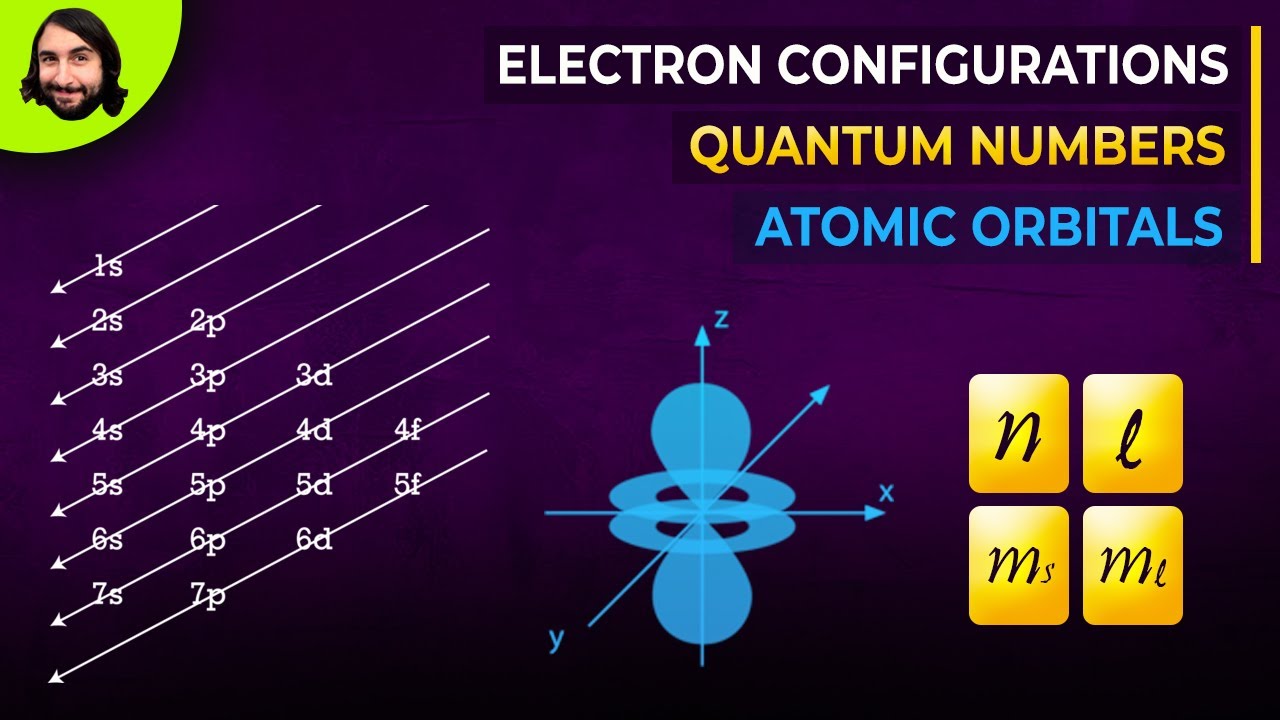
- Four quantum numbers define the location and energy of electrons: principal (n), angular momentum (l), magnetic (ml), and spin (ms).
- The Aufbau principle dictates the order in which electrons fill orbitals, starting with the lowest energy levels.
- Hund's rule states that electrons fill each orbital within a subshell singly before doubling up.
- Electron configurations and orbital diagrams visually represent the arrangement of electrons in an atom.
- Paramagnetic atoms have unpaired electrons and are attracted to magnetic fields, while diamagnetic atoms have all electrons paired and are not affected.
Introduction to Quantum Numbers
The video introduces the concept of quantum numbers, which define the location and energy of electrons within an atom. It explains that electrons behave as both particles and waves, and their arrangement is described by four quantum numbers that correspond to different atomic orbitals (s, p, d, and f). These orbitals represent regions of probability where electrons can be found, with each orbital holding up to two electrons.
The Principal Quantum Number (n)
The principal quantum number, denoted as "n," is explained as a positive integer representing the energy level of an electron. Higher values of "n" indicate that the electron is further from the nucleus and has higher energy. Each orbital has an "n" value, determining its energy level.
The Angular Momentum Quantum Number (l)
The angular momentum quantum number, "l," is described as ranging from 0 to n-1 and determines the shape of the orbital. When l = 0, it represents spherical s orbitals (one per energy level). When l = 1, it represents p orbitals, which are lobe-shaped and extend along three axes (three per energy level). The video further explains that l = 2 corresponds to d orbitals (five per energy level), and l = 3 corresponds to f orbitals (seven per energy level), both with more complex shapes.
The Magnetic Quantum Number (ml)
The magnetic quantum number, represented as m sub l, determines the number of orbitals of a specific type within an energy level. Its values range from -l to +l, including 0. For l = 0 (s orbitals), m sub l is 0, indicating one s orbital per energy level. For l = 1 (p orbitals), m sub l can be -1, 0, or 1, resulting in three p orbitals. Similarly, l = 2 (d orbitals) yields five d orbitals, and l = 3 (f orbitals) yields seven f orbitals.
The Spin Quantum Number (ms)
The spin quantum number, m sub s, is explained as having only two possible values: +1/2 or -1/2, representing the spin of an electron. The Pauli exclusion principle states that no two electrons in an atom can have the same set of all four quantum numbers. This principle dictates that each orbital can hold a maximum of two electrons, each with opposite spins.
Describing Quantum Numbers and Orbitals
The video provides examples of describing different sets of quantum numbers and their corresponding orbitals. When n=1, l=0, and m sub l =0, it describes the 1s orbital, which can hold two electrons with opposite spins. Hydrogen and helium atoms occupy this orbital. For n=2, l can be 0 (2s orbital) or 1 (2p orbitals, with m sub l being -1, 0, or 1). The outermost electrons in the second row of the periodic table occupy these orbitals. When n=3, l can be 0 (3s orbital), 1 (3p orbitals), or 2 (3d orbitals), which are used by larger atoms to accommodate their electrons.
Aufbau Principle and Electron Configuration
The Aufbau principle is introduced as the rule that dictates the order in which electrons fill atomic orbitals, starting with the lowest energy levels. Orbitals further from the nucleus have higher potential energy. The filling order is 1s, 2s, 2p, 3s, 3p, and so on. This principle is used to determine the electron configuration of any atom. For example, a neutral chlorine atom with 17 electrons fills the 1s, 2s, 2p, and 3s orbitals completely, with the remaining five electrons occupying the 3p orbitals.
Hund's Rule and Determining Electron Configuration
Hund's rule is explained, stating that when filling orbitals of equal energy, electrons are placed singly into each orbital before any orbital is doubly occupied. This maximizes the total spin. For chlorine, this results in the electron configuration 1s² 2s² 2p⁶ 3s² 3p⁵. The numbers before the letters indicate the n value, and the numbers after the letters indicate the number of electrons in each type of orbital. The video also describes a shortcut using the periodic table, where the s-block, p-block, d-block, and f-block correspond to the filling of s, p, d, and f orbitals, respectively.
Using the Periodic Table for Electron Configuration
The video explains how to use the periodic table to quickly determine electron configurations. By moving left to right and up to down, each element adds one more electron. For chlorine, the 1s orbital is full (1s²). In the second row (n=2), the 2s orbital is filled (2s²), and the 2p orbitals are filled (2p⁶). In the third row, the 3s orbital is filled (3s²), and five electrons are in the 3p orbitals (3p⁵). A shorthand notation involves using the noble gas from the previous row in brackets to represent the core electrons, followed by the valence electrons.
Orbital Diagrams and Magnetic Properties
Orbital diagrams are introduced as visual representations of how orbitals are filled, following Hund's rule. Atoms with unpaired electrons in their orbital diagrams are paramagnetic and are attracted to magnetic fields. Atoms with all electrons paired are diamagnetic and are not affected by magnetic fields.
Summary of Quantum Numbers and Principles
The video summarizes the key points: n represents the energy level, l represents the type of orbital, m sub l represents the specific orbital within a set, and m sub s represents the spin. Each electron in an atom has a unique set of quantum numbers, and atoms fill orbitals according to the Aufbau principle until all electrons are accommodated.