Resumen Breve
Este video explica cómo realizar la suma y resta de vectores utilizando tanto el método analítico como el gráfico (método del paralelogramo). Se detalla cómo sumar y restar vectores A y B, primero analíticamente sumando o restando sus componentes, y luego gráficamente ubicando los vectores en un plano y utilizando el método del paralelogramo para encontrar el vector resultante.
- Suma de vectores A + B se realiza sumando las componentes correspondientes.
- Resta de vectores A - B se realiza sumando el vector A con el opuesto del vector B.
- El método gráfico del paralelogramo implica dibujar vectores paralelos a los originales desde los extremos para encontrar el vector resultante.
Introducción
El video introduce el tema de la suma y resta de vectores utilizando métodos analíticos y gráficos, específicamente el método del paralelogramo. Se presentan dos vectores, A y B, y el objetivo es calcular A + B y A - B mediante ambos métodos.
Suma de Vectores: Método Analítico
Se explica cómo sumar los vectores A (5, -3) y B (-2, 4) analíticamente. Esto se hace sumando las componentes x y y de cada vector por separado. La componente x de A (5) se suma con la componente x de B (-2), y la componente y de A (-3) se suma con la componente y de B (4). El resultado es un nuevo vector (3, 1), que representa la suma de A + B.
Suma de Vectores: Método Gráfico
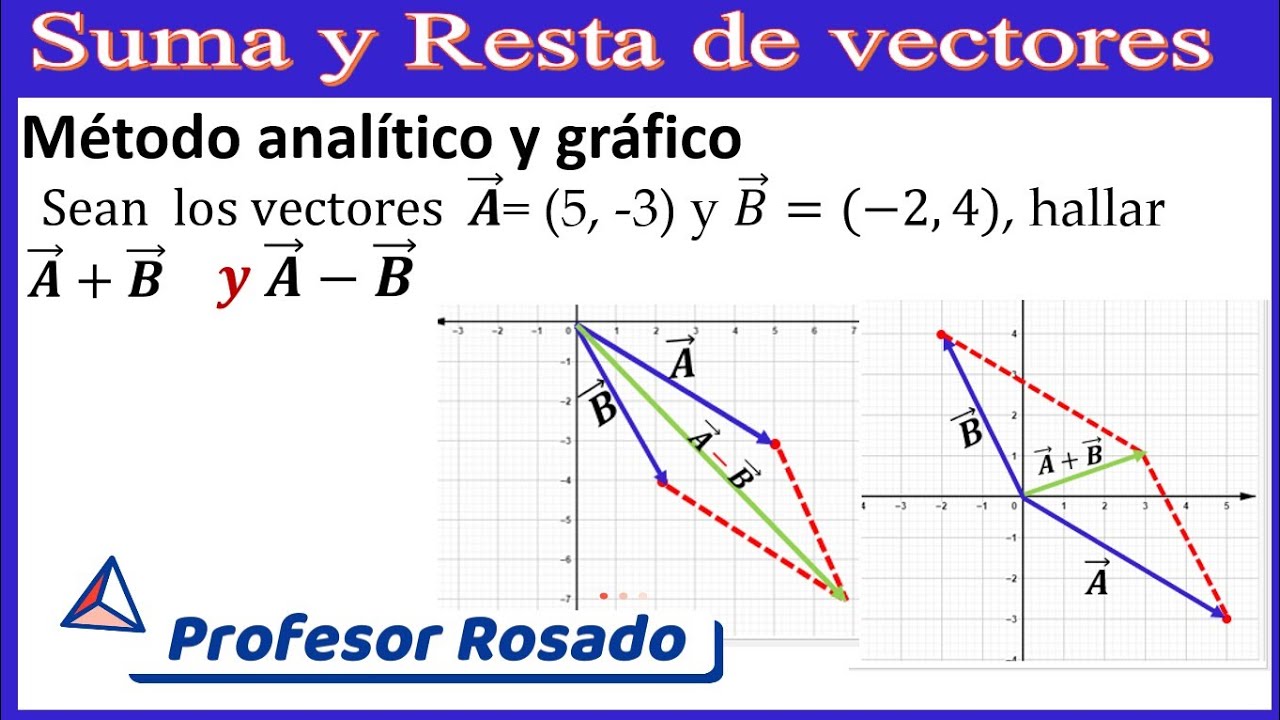
Se explica cómo representar gráficamente los vectores A (5, -3) y B (-2, 4) en un plano cartesiano. El vector A se dibuja desde el origen (0,0) hasta el punto (5, -3), y el vector B desde el origen hasta el punto (-2, 4). Para encontrar la suma gráficamente usando el método del paralelogramo, se dibuja una línea paralela al vector B desde el extremo del vector A, y una línea paralela al vector A desde el extremo del vector B. El punto donde se cruzan estas líneas paralelas determina el extremo del vector resultante A + B, que va desde el origen hasta este punto de intersección, que debe ser el punto (3,1).
Resta de Vectores: Introducción
Se introduce la resta de vectores A - B, explicando que es similar a la suma, pero implica sumar el vector A con el opuesto del vector B. El opuesto de un vector se obtiene cambiando el signo de sus componentes.
Resta de Vectores: Método Analítico
Se explica cómo encontrar el opuesto del vector B (-2, 4), que es -B (2, -4). Luego, se suma el vector A (5, -3) con el opuesto de B (2, -4). Esto se hace sumando las componentes x y y de cada vector por separado: (5 + 2) y (-3 + -4). El resultado es el vector (7, -7), que representa la resta A - B.
Resta de Vectores: Método Gráfico
Se explica cómo representar gráficamente la resta de vectores A - B. Primero, se dibuja el vector A (5, -3) desde el origen hasta el punto (5, -3). Luego, se dibuja el vector -B (2, -4) desde el origen hasta el punto (2, -4). Para encontrar la resta gráficamente usando el método del paralelogramo, se dibuja una línea paralela al vector -B desde el extremo del vector A, y una línea paralela al vector A desde el extremo del vector -B. El punto donde se cruzan estas líneas paralelas determina el extremo del vector resultante A - B, que va desde el origen hasta este punto de intersección, que debe ser el punto (7, -7).
Conclusión
Se concluye que la suma y resta de vectores se pueden realizar tanto analítica como gráficamente utilizando el método del paralelogramo. Se destaca la importancia de entender el concepto del opuesto de un vector al realizar la resta.