Breve Resumen
Este video es una introducción al concepto de distancia entre dos puntos en el plano cartesiano. Se explica cómo ubicar puntos en el plano, cómo calcular la distancia entre puntos en líneas horizontales y verticales contando unidades, y se advierte sobre el error común de aplicar este método a líneas oblicuas. Además, se enfatiza que las distancias siempre son positivas y se introduce la idea de que la escala del plano cartesiano afecta la medición de las distancias.
- Se explica cómo ubicar puntos en el plano cartesiano.
- Se calcula la distancia entre puntos en líneas horizontales y verticales.
- Se advierte sobre el error común de aplicar este método a líneas oblicuas.
Saludo
El profesor Alex da la bienvenida al curso de ecuación de la recta y presenta una introducción al concepto de distancia entre dos puntos.
Conceptos que debes saber
Se introduce el concepto de distancia entre dos puntos en el plano cartesiano. Se explica que la distancia es la longitud de la recta que une esos dos puntos. Se menciona que se comenzará con ejercicios sencillos para facilitar la comprensión.
Solución del ejemplo
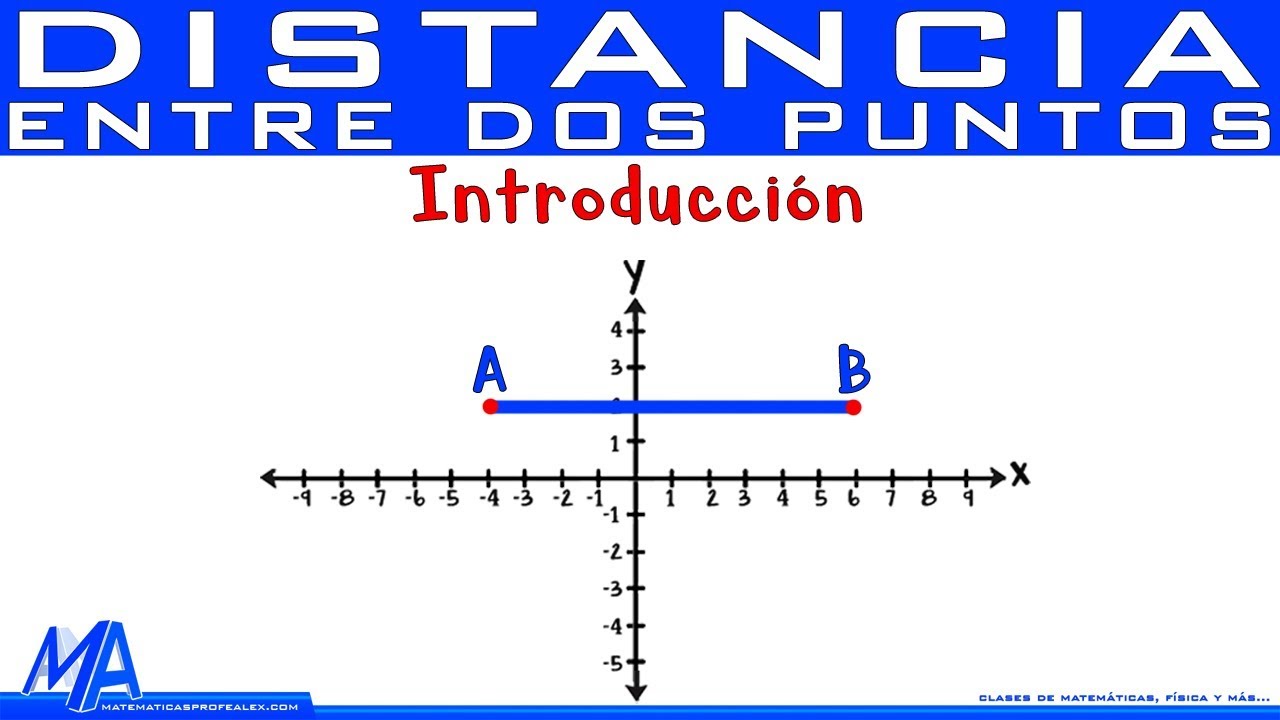
Se explica cómo ubicar los puntos A(2,1) y B(5,1) en el plano cartesiano, recordando que la primera coordenada corresponde al eje x y la segunda al eje y. Se traza la recta que une estos dos puntos y se calcula su longitud contando los cuadritos que la componen, determinando que la distancia entre A y B es de 3 unidades. Se aclara que cada cuadrito representa una unidad.
Solución del ejemplo 2
Se presenta un segundo ejemplo con los puntos C(-3,4) y D(-3,-2). Se ubican los puntos en el plano cartesiano y se traza la recta que los une. Se calcula la distancia entre C y D contando los cuadritos, obteniendo un resultado de 6 unidades. Se enfatiza que las distancias siempre son positivas, independientemente de la dirección en que se cuente. Se explica que la escala del plano cartesiano puede variar, utilizando unidades de dos cuadritos en lugar de uno, y cómo esto afecta la medición de las distancias. Se advierte sobre el error de intentar medir la distancia entre puntos que no están en líneas horizontales o verticales contando cuadritos, ya que este método solo es válido para líneas rectas en esas direcciones.
Ejercicio de práctica
Se propone un ejercicio de práctica donde se dan cuatro puntos (A, B, C, D) y se pide calcular las distancias entre A y B, B y D, C y D, A y C, y B y C. Se muestran las soluciones, indicando que las distancias entre puntos en líneas horizontales o verticales se pueden calcular contando cuadritos, pero que para las líneas oblicuas se necesita otro método que se verá en el siguiente video. Se observa que la recta entre A y B mide 8 unidades, y las rectas que unen A con D y B con C miden más de 8 unidades. El video finaliza invitando a ver el curso completo y a suscribirse al canal.