Resumen Breve
Este video explica cómo calcular la distancia entre dos puntos utilizando el método gráfico. Se basa en la formación de triángulos rectángulos y la aplicación del teorema de Pitágoras para encontrar la longitud de la hipotenusa, que representa la distancia entre los puntos. Incluye ejemplos prácticos y un ejercicio para practicar.
- Se utiliza el teorema de Pitágoras para calcular la distancia.
- Se explica cómo formar triángulos rectángulos utilizando los puntos dados.
- Se proporcionan ejemplos prácticos para comprender el concepto.
Saludo
El video comienza con un saludo y una introducción al tema del curso sobre la ecuación de la recta, específicamente cómo encontrar la distancia entre dos puntos utilizando el método gráfico.
Conceptos que debes saber
El video explica que para encontrar la distancia entre dos puntos en un plano cartesiano, se debe trazar una recta entre los dos puntos y luego formar un triángulo rectángulo donde esta recta sea la hipotenusa. Se pueden formar dos triángulos rectángulos diferentes, pero ambos serán semejantes y tendrán las mismas medidas en sus catetos.
Solución del ejemplo
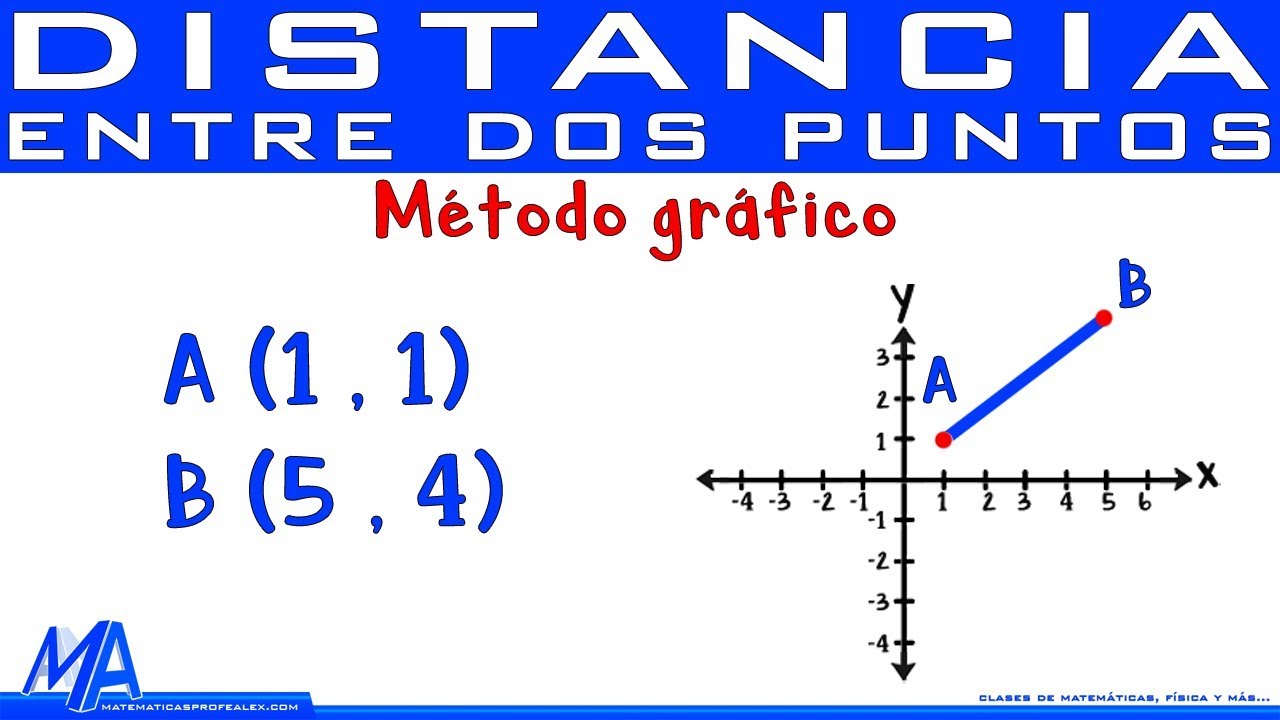
Se explica cómo encontrar la distancia entre los puntos A(1,1) y B(5,4). Se forma un triángulo rectángulo con la recta que une los puntos A y B como hipotenusa. Los catetos del triángulo miden 3 y 4 unidades respectivamente. Aplicando el teorema de Pitágoras (distancia² = 3² + 4²), se calcula la distancia como la raíz cuadrada de 25, que es 5 unidades.
Solución del ejemplo 2
Se explica cómo encontrar la distancia entre los puntos C(3,-2) y D(-3,5). Se forma un triángulo rectángulo con la recta que une los puntos C y D como hipotenusa. Los catetos del triángulo miden 7 y 6 unidades respectivamente. Aplicando el teorema de Pitágoras (distancia² = 7² + 6²), se calcula la distancia como la raíz cuadrada de 85, que es aproximadamente 9.2 unidades.
Ejercicio de práctica
Se proponen tres ejercicios para practicar el cálculo de la distancia entre puntos: A y B, C y D, y E y F. Se proporcionan las respuestas: la distancia entre A y B es 10, entre C y D es la raíz cuadrada de 29 (aproximadamente 5.38), y entre E y F es 5 (este último sin necesidad de formar un triángulo por ser una línea vertical).