Resumen Breve
Este video explica cómo determinar el dominio y el rango de una función a partir de su gráfica. Se enfoca en identificar los valores mínimos y máximos en los ejes horizontal (x) y vertical (y), respectivamente, considerando si los extremos están incluidos o excluidos (intervalos cerrados o abiertos). Se analizan ejemplos con diferentes tipos de gráficas, incluyendo funciones limitadas, semicírculos y rectas acotadas, explicando cómo los puntos rellenos o huecos en la gráfica afectan la definición del dominio y rango.
- El dominio se encuentra analizando el eje horizontal (x).
- El rango se encuentra analizando el eje vertical (y).
- Intervalos cerrados indican que el valor extremo está incluido, mientras que los intervalos abiertos indican que está excluido.
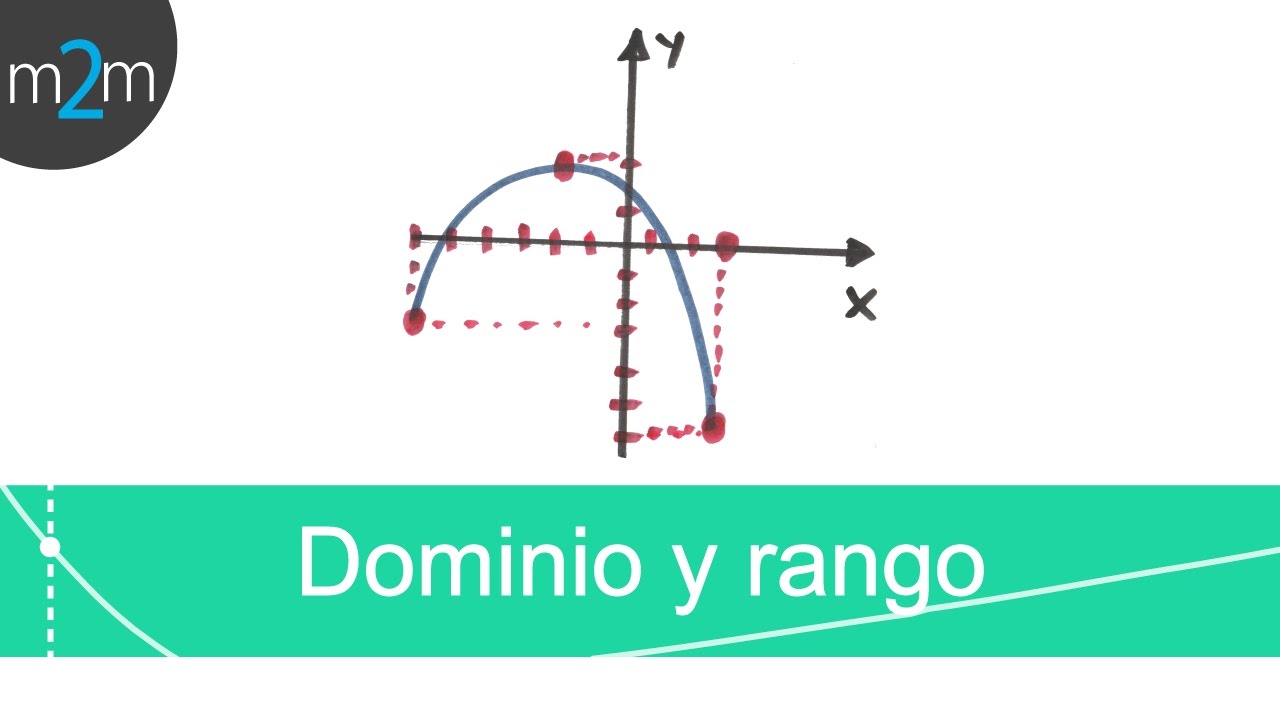
Dominio y Rango de una Función con Gráfica Limitada
Para hallar el dominio y rango de una función dada en forma de gráfica, es importante observar si la gráfica está limitada. En este caso, la gráfica está limitada tanto en la parte inferior como en la superior. El dominio se obtiene trabajando sobre el eje horizontal (eje x). Se identifica el valor más pequeño (a la izquierda), que es -6, y se observa que sí pertenece a la función (punto relleno), por lo que se toma un intervalo cerrado. Para el valor máximo de x, se mueve a la derecha hasta 6, pero este punto no pertenece a la función (punto hueco), indicando un intervalo abierto. Para el rango, se analiza el eje vertical (eje y). El valor mínimo es -7, que sí pertenece a la función (punto relleno), indicando un intervalo cerrado. El valor máximo es 8, pero no pertenece a la función (punto hueco), indicando un intervalo abierto.
Dominio y Rango de un Semicírculo
Para hallar el dominio de un semicírculo, se enfoca en el eje horizontal (x). El valor más a la izquierda es -7, que está relleno, indicando un intervalo cerrado. El valor más a la derecha es +7, también relleno, indicando un intervalo cerrado. Para el rango, se analiza el eje vertical (y). El valor mínimo es 0, ya que hay puntos en x que existen en y, y el valor máximo es +7, que también es un intervalo cerrado.
Dominio y Rango de una Función con Intervalos Abiertos
Para hallar el dominio, se enfoca en el eje horizontal. El valor menor es -5, pero no se puede tomar (intervalo abierto). El valor máximo es 2, tampoco se puede tomar (intervalo abierto). Para el rango, se analiza el eje vertical. El valor mínimo es -7 (intervalo abierto), y el valor máximo es 3 (intervalo cerrado).
Dominio y Rango de una Recta Acotada
Para definir el dominio de una recta acotada, se enfoca en el eje horizontal. Debido a que está acotada, se define un extremo en el lado izquierdo en -5, que se está tomando (intervalo cerrado). Del lado derecho, la recta va hasta el infinito positivo (intervalo abierto). Para el rango, se analiza el eje vertical. La recta está acotada en la parte inferior en -3 (intervalo cerrado), y crece de manera infinita para el lado positivo (intervalo abierto).