Breve Resumen
Este video introduce el concepto de parábolas, explicando su forma, terminología básica y cómo se relacionan con ecuaciones cuadráticas. Se definen términos como "abrir hacia arriba" o "abrir hacia abajo", vértice, eje de simetría e intersecciones con los ejes X e Y.
- Las parábolas pueden abrir hacia arriba o hacia abajo.
- El vértice es el punto máximo o mínimo de la parábola.
- El eje de simetría divide la parábola en dos mitades iguales.
- Las intersecciones con los ejes X e Y son puntos donde la parábola cruza estos ejes.
Introducción a las Parábolas
El video comienza introduciendo las parábolas como curvas comunes en matemáticas. Se menciona el origen de la palabra "parábola" del griego, posiblemente relacionada con la trayectoria de objetos arrojados. El objetivo del video es proporcionar una comprensión intuitiva de las parábolas y su terminología, antes de abordarlas algebraicamente en futuros videos.
Apertura de la Parábola: Hacia Arriba o Hacia Abajo
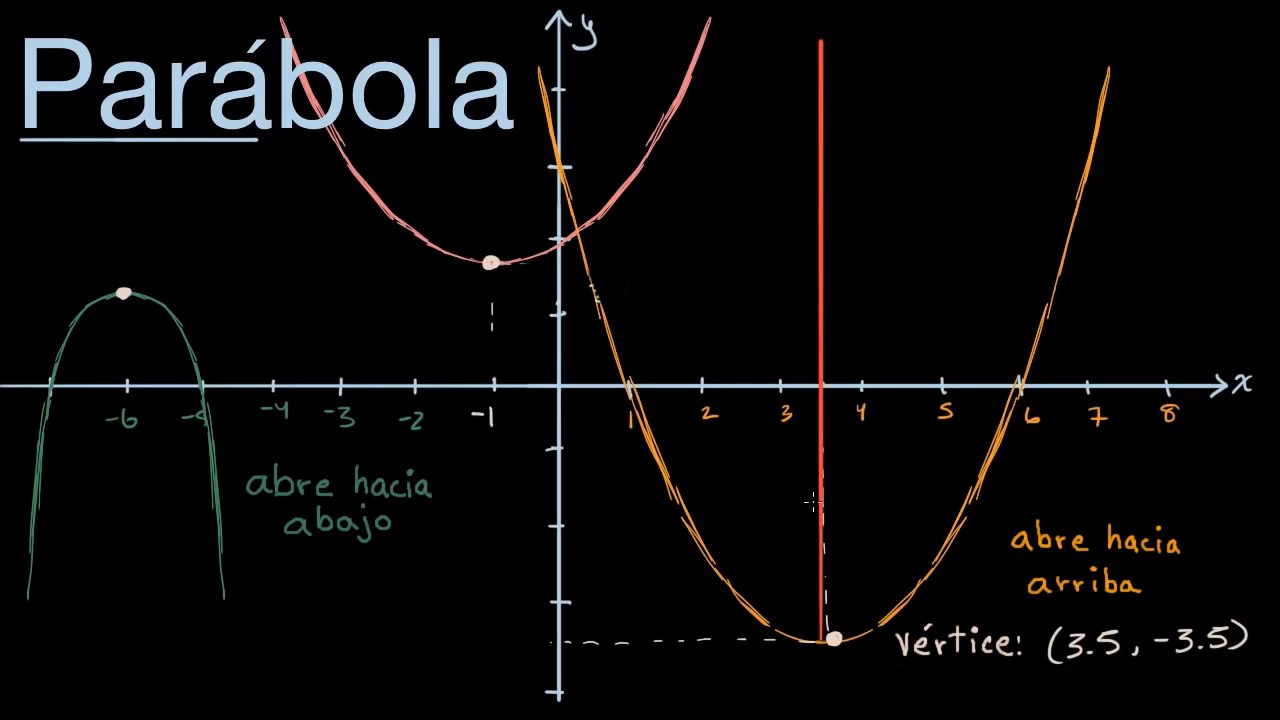
Se explica que las parábolas pueden "abrir hacia arriba" (con forma de U) o "abrir hacia abajo" (con forma de U invertida). Esta característica visual es fundamental para describir y entender la orientación de la parábola en el plano cartesiano. Se dan ejemplos visuales con parábolas de diferentes colores para ilustrar ambos casos.
Vértice y Eje de Simetría
El vértice se define como el punto máximo (si la parábola abre hacia abajo) o mínimo (si la parábola abre hacia arriba) de la curva. Se muestra cómo identificar el vértice en las gráficas y se dan ejemplos de sus coordenadas. Además, se introduce el concepto de eje de simetría, una línea recta que divide la parábola en dos mitades simétricas, pasando siempre por el vértice. Se explica cómo encontrar la ecuación del eje de simetría (x = constante) y se ilustra con ejemplos gráficos.
Intersecciones con los Ejes
Se explica el concepto de intersecciones con los ejes X e Y. La intersección con el eje Y es el punto donde la parábola cruza el eje vertical. La intersección con el eje X (o las intersecciones, ya que puede haber dos) son los puntos donde la parábola cruza el eje horizontal. Se destaca que las intersecciones con el eje X son simétricas con respecto al eje de simetría. Se menciona que no todas las parábolas intersecan el eje X.
Ecuaciones Cuadráticas y Parábolas
El video concluye mencionando que las parábolas se representan mediante ecuaciones cuadráticas, que involucran términos de segundo grado (x²). Se dan ejemplos de ecuaciones cuadráticas simples (y = x²) y más complejas (y = 2x² - 5x + 7), anticipando que en futuros videos se explorarán estas ecuaciones con mayor detalle.