Breve Resumen
Este video introduce el movimiento parabólico, también conocido como movimiento de proyectiles o bidimensional, explicando cómo analizarlo mediante componentes vectoriales. Se desglosan las ecuaciones clave para describir el movimiento en los ejes x e y, considerando la velocidad constante en el eje x y la influencia de la gravedad en el eje y. Además, se derivan fórmulas para el tiempo de subida y el alcance máximo, culminando con un resumen de las ecuaciones fundamentales para resolver problemas de movimiento parabólico.
- El movimiento parabólico se analiza descomponiendo la velocidad en componentes x e y.
- La velocidad en el eje x es constante, mientras que en el eje y varía debido a la gravedad.
- Se presentan y explican las ecuaciones para el desplazamiento en ambos ejes, la velocidad en el eje y, el tiempo de subida y el alcance máximo.
Introducción al Movimiento Parabólico
El video inicia una serie sobre movimiento parabólico, también conocido como movimiento de proyectiles o bidimensional. Se explica que este tipo de movimiento se caracteriza por tener componentes tanto horizontal (x) como vertical (y), como el de una pelota que es golpeada y se desplaza hacia arriba y hacia la derecha. Para analizar este movimiento, se utilizan componentes vectoriales, descomponiendo el movimiento en sus componentes unidimensionales x e y.
Componentes de la Velocidad y Aceleración
Se explica que la componente x de la velocidad (Vx) es constante, lo que implica una aceleración de cero en esa dirección, similar al movimiento rectilíneo uniforme. Por otro lado, la componente y de la velocidad (Vy) varía con el tiempo debido a la gravedad, que actúa en dirección vertical negativa, recordando al movimiento de caída libre. A medida que el objeto asciende, Vy disminuye hasta llegar a cero en la cima del arco, para luego aumentar al descender.
Descomposición de la Velocidad Inicial
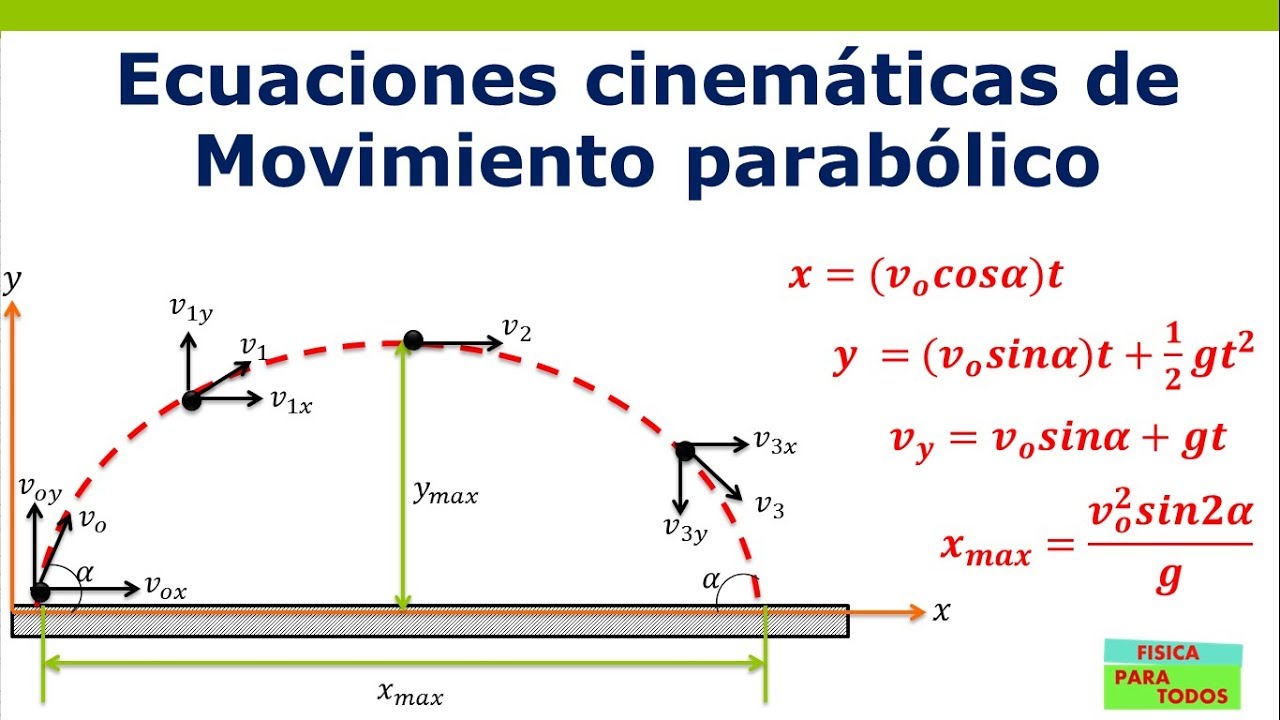
Se presenta un esquema donde una pelota es lanzada con una velocidad inicial (V0) a un ángulo α con respecto al eje horizontal. Esta velocidad inicial se descompone en sus componentes Vx y Vy. Se explica cómo Vx permanece constante a lo largo de la trayectoria, mientras que Vy disminuye al ascender, se hace cero en el punto más alto y luego aumenta al descender, cambiando de dirección.
Trigonometría Aplicada a la Descomposición de Vectores
Se revisan conceptos básicos de trigonometría para descomponer el vector velocidad inicial. Utilizando un triángulo rectángulo, se recuerda que el coseno de un ángulo es igual al lado adyacente sobre la hipotenusa, y el seno es igual al lado opuesto sobre la hipotenusa. De esta manera, se establece que Vx = V0 * cos(α) y Vy = V0 * sen(α).
Ecuaciones del Movimiento en el Eje X
Dado que la velocidad en el eje x es constante, se utiliza la ecuación del movimiento rectilíneo uniforme: desplazamiento = velocidad inicial * tiempo. Reemplazando Vx por V0 * cos(α), se obtiene la ecuación para el desplazamiento en x: x = V0 * cos(α) * t.
Ecuaciones del Movimiento en el Eje Y
En el eje y, se utiliza la ecuación de caída libre: desplazamiento en y = velocidad inicial en y * tiempo + 1/2 * gravedad * tiempo al cuadrado. Reemplazando Vy por V0 * sen(α), se obtiene la ecuación para el desplazamiento en y: y = V0 * sen(α) * t + 1/2 * g * t^2. También se presenta la ecuación de velocidad final en y: Vy = V0 * sen(α) + g * t.
Tiempo de Subida y Alcance Máximo
Se define el tiempo de subida (Ts) como el tiempo que tarda el objeto en alcanzar su máxima altura, donde Vy = 0. Utilizando la ecuación de velocidad final en y, se deriva la fórmula para el tiempo de subida: Ts = V0 * sen(α) / g. Luego, se busca una ecuación para el alcance máximo (Xmáx), utilizando la ecuación del desplazamiento en x y considerando que el tiempo total es dos veces el tiempo de subida.
Derivación de la Fórmula del Alcance Máximo
Sustituyendo el tiempo de subida en la ecuación del alcance máximo y utilizando identidades trigonométricas (2 * sen(α) * cos(α) = sen(2α)), se llega a la fórmula final para el alcance máximo: Xmáx = (V0^2 * sen(2α)) / g. Se enfatiza que esta fórmula es válida siempre y cuando el punto de partida y el punto de llegada estén sobre la misma línea horizontal.
Resumen de Ecuaciones Clave
Se resumen las cuatro ecuaciones fundamentales para la cinemática del movimiento parabólico:
- Desplazamiento en x: x = V0 * cos(α) * t
- Desplazamiento en y: y = V0 * sen(α) * t + 1/2 * g * t^2
- Velocidad en y: Vy = V0 * sen(α) + g * t
- Alcance máximo: Xmáx = (V0^2 * sen(2α)) / g (válida solo si el punto de partida y llegada están en la misma línea horizontal)