Resumen Breve
Este video explica el concepto de razón de cambio instantánea, diferenciándolo de la razón de cambio promedio. Se introduce la idea de un incremento infinitesimal y cómo se relaciona con la pendiente de una recta tangente a una curva en un punto específico. Además, se explica cómo calcular la pendiente de la recta normal y se resuelven ejemplos prácticos aplicando estos conceptos.
- La razón de cambio instantánea se define como el límite de la razón de cambio promedio cuando el intervalo de tiempo tiende a cero.
- La pendiente de la recta tangente a una curva en un punto representa la razón de cambio instantánea en ese punto.
- La recta normal es perpendicular a la recta tangente en el punto de tangencia.
Introducción al Concepto de Razón de Cambio Instantánea
Se plantea un problema sobre un ciclista cuya distancia recorrida está dada por una función del tiempo. Se busca determinar la velocidad media en un intervalo de tiempo y la velocidad en un instante específico. Se diferencia la razón de cambio promedio, que se calcula en un intervalo, de la razón de cambio instantánea, que se refiere a un momento específico. Se destaca la necesidad de considerar un valor de tiempo extremadamente pequeño para calcular la velocidad en un instante.
Incrementos y Razón de Cambio Promedio
Se repasa el concepto de incremento de una variable y cómo se calcula la razón de cambio promedio como el cociente entre el incremento de la variable dependiente (y) y el incremento de la variable independiente (x). Se explica que la razón de cambio promedio mide la variación de una función en un intervalo. Se menciona que la razón de cambio se entiende como la medida de cambio de una variable con respecto a otra, ejemplificando con velocidad, aceleración, densidad, pendiente y corriente eléctrica.
Definición y Visualización de la Razón de Cambio Instantánea
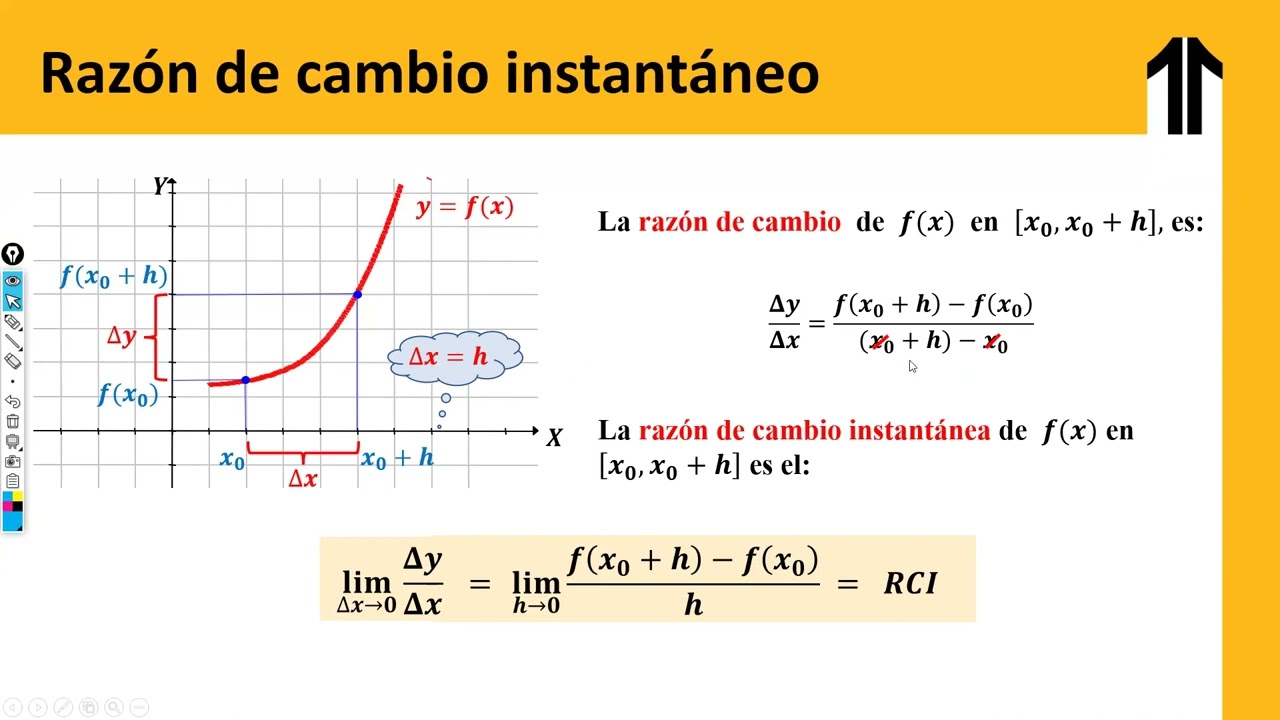
Se explica que la razón de cambio instantánea se diferencia de la razón de cambio promedio en que el incremento en el valor de x es extremadamente pequeño, tendiendo a cero. Se utiliza la analogía de observar una pelota en movimiento y el parpadeo para ilustrar un instante de tiempo. Se presenta la fórmula de la razón de cambio instantánea como un límite, donde h (el incremento de x) tiende a cero.
Interpretación Geométrica: Recta Secante y Tangente
Se explica la interpretación geométrica de la razón de cambio instantánea utilizando una curva y rectas secantes y tangentes. La pendiente de la recta secante que corta la curva en dos puntos representa la razón de cambio promedio. A medida que los dos puntos de la recta secante se acercan hasta coincidir, la recta secante se convierte en una recta tangente que toca la curva en un solo punto. La pendiente de esta recta tangente representa la razón de cambio instantánea en ese punto.
Ejemplo 1: Pendiente de la Recta Tangente y Normal a una Parábola
Se resuelve un ejercicio para hallar la pendiente de la recta tangente y la recta normal a la gráfica de la función f(x) = x² en el punto (1,1). Se utiliza la definición de la pendiente de la recta tangente como el límite de la razón de cambio cuando h tiende a cero. Se calcula la pendiente de la recta tangente como 2. Luego, se utiliza la propiedad de que el producto de las pendientes de dos rectas perpendiculares es -1 para hallar la pendiente de la recta normal, que resulta ser -1/2.
Ejemplo 2: Pendiente de la Recta Tangente y Normal a una Función Cúbica
Se resuelve un segundo ejercicio para hallar la pendiente de la recta tangente y la recta normal a la gráfica de la función f(x) = x³ - 12x - 5 en el punto (-2, 11). Se aplica nuevamente la definición de la pendiente de la recta tangente como un límite. Tras simplificar la expresión y evaluar el límite, se encuentra que la pendiente de la recta tangente es 0. Esto indica que la recta tangente es horizontal en ese punto. Como la recta normal es perpendicular a la recta tangente, su pendiente no existe (o se considera infinita) ya que sería una línea vertical.
Ejemplo 3: Razón de Cambio Instantánea de la Temperatura
Se presenta un problema donde la temperatura en un punto de experimentación agrícola está dada por una función del tiempo. Se pide determinar la razón de cambio instantánea de la temperatura a las 4 de la mañana. Se aplica la definición de razón de cambio instantánea como un límite. Después de simplificar la expresión y evaluar el límite, se encuentra que la razón de cambio instantánea es -1.92 grados centígrados por hora. Esto indica que la temperatura está disminuyendo a una tasa de 1.92 grados centígrados por hora en ese instante.
Conclusiones y Aplicaciones
Se resume lo aprendido en la sesión, destacando la importancia de la razón de cambio instantánea y su relación con los instantes de tiempo. Se mencionan las dificultades comunes en la comprensión del concepto y la necesidad de dominar otros aspectos matemáticos como el cálculo de pendientes de rectas tangentes y normales. Se mencionan aplicaciones en física, como la cinemática y la dinámica, y se relaciona la razón de cambio instantánea con el concepto de derivada, que se estudiará en detalle en cursos de cálculo. Se proporcionan referencias bibliográficas para profundizar en el tema.