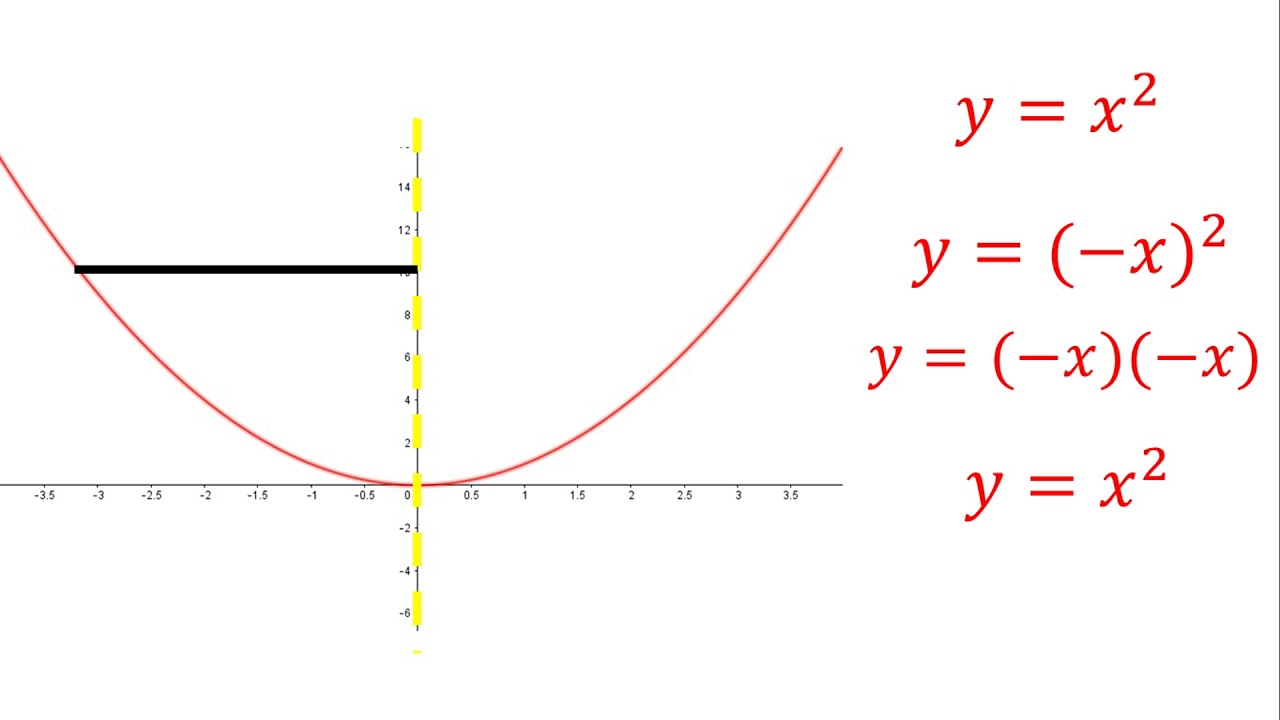Resumen Breve
Este video explica cómo identificar la simetría en las gráficas de ecuaciones con respecto a los ejes x e y, y al origen. Se detalla el método para determinar la simetría sustituyendo variables en la ecuación y analizando si la ecuación resultante es idéntica a la original.
- Simetría con respecto al eje y: Sustituir x por -x.
- Simetría con respecto al eje x: Sustituir y por -y.
- Simetría con respecto al origen: Sustituir tanto x como y por sus negativos.
Simetría con respecto al eje Y
Una gráfica es simétrica con respecto al eje y si al trazar una línea vertical sobre este eje, la gráfica se divide en dos partes que son imágenes especulares una de la otra. Para determinar algebraicamente si una ecuación es simétrica con respecto al eje y, se sustituye x por -x en la ecuación original. Si la ecuación resultante es idéntica a la original, entonces la gráfica es simétrica con respecto al eje y. Por ejemplo, la ecuación y = x² es simétrica con respecto al eje y porque al sustituir x por -x, la ecuación no se altera.
Simetría con respecto al eje X
Una gráfica es simétrica con respecto al eje x si al trazar una línea horizontal sobre este eje, la gráfica se divide en dos partes que son imágenes especulares una de la otra. Para verificar algebraicamente la simetría con respecto al eje x, se sustituye y por -y en la ecuación original. Si la ecuación resultante es la misma que la original, entonces la gráfica es simétrica con respecto al eje x. Por ejemplo, y² = 9x es simétrica con respecto al eje x porque al sustituir y por -y, la ecuación no cambia.
Simetría con respecto al origen
Una gráfica es simétrica con respecto al origen si, al trazar una línea desde el origen hasta un punto en la gráfica y extender esa línea en la dirección opuesta, se encuentra otro punto en la gráfica. Para determinar algebraicamente si una ecuación es simétrica con respecto al origen, se sustituyen tanto x como y por sus negativos (-x y -y) en la ecuación original. Si después de simplificar, la ecuación resultante es idéntica a la original, entonces la gráfica es simétrica con respecto al origen. Por ejemplo, y = (1/2)x³ es simétrica con respecto al origen.
Consideraciones adicionales sobre la simetría
Las simetrías no son mutuamente excluyentes; una ecuación puede ser simétrica con respecto al eje y, al eje x y al origen. Sin embargo, también es posible que una ecuación no presente simetría con respecto a ninguno de estos elementos.