Resumen Breve
Este video explica cómo resolver sistemas de ecuaciones lineales de 2x2 utilizando el método gráfico. El método implica graficar cada ecuación como una línea recta y encontrar el punto donde se cruzan, cuyas coordenadas representan la solución del sistema. Se enfatiza la importancia de verificar la solución reemplazando los valores de x e y en las ecuaciones originales.
- Se utiliza una tabla de valores para graficar las ecuaciones.
- La solución del sistema es el punto de intersección de las dos rectas.
- Se verifica la solución reemplazando los valores en las ecuaciones originales.
Saludo
El video da la bienvenida a los espectadores a un curso sobre la solución de sistemas de ecuaciones lineales de 2x2, enfocándose en el método gráfico. Se anticipa que este primer ejemplo será sencillo, con ejercicios más complejos en videos futuros.
Solución del ejemplo
Para resolver un sistema de ecuaciones por el método gráfico, se deben graficar las ecuaciones lineales. Cada ecuación, al ser graficada, resulta en una línea recta. La solución del sistema es el punto donde estas dos líneas se intersectan. Para graficar, se utiliza una tabla de valores, asignando valores a 'x' y calculando los correspondientes valores de 'y'. Se recomienda usar al menos tres puntos para asegurar la precisión de la línea recta. En este ejemplo, se eligen los valores 0, 1 y 2 para 'x' debido a su simplicidad. Estos valores se sustituyen en cada ecuación para encontrar los valores correspondientes de 'y', completando así la tabla de valores necesaria para graficar.
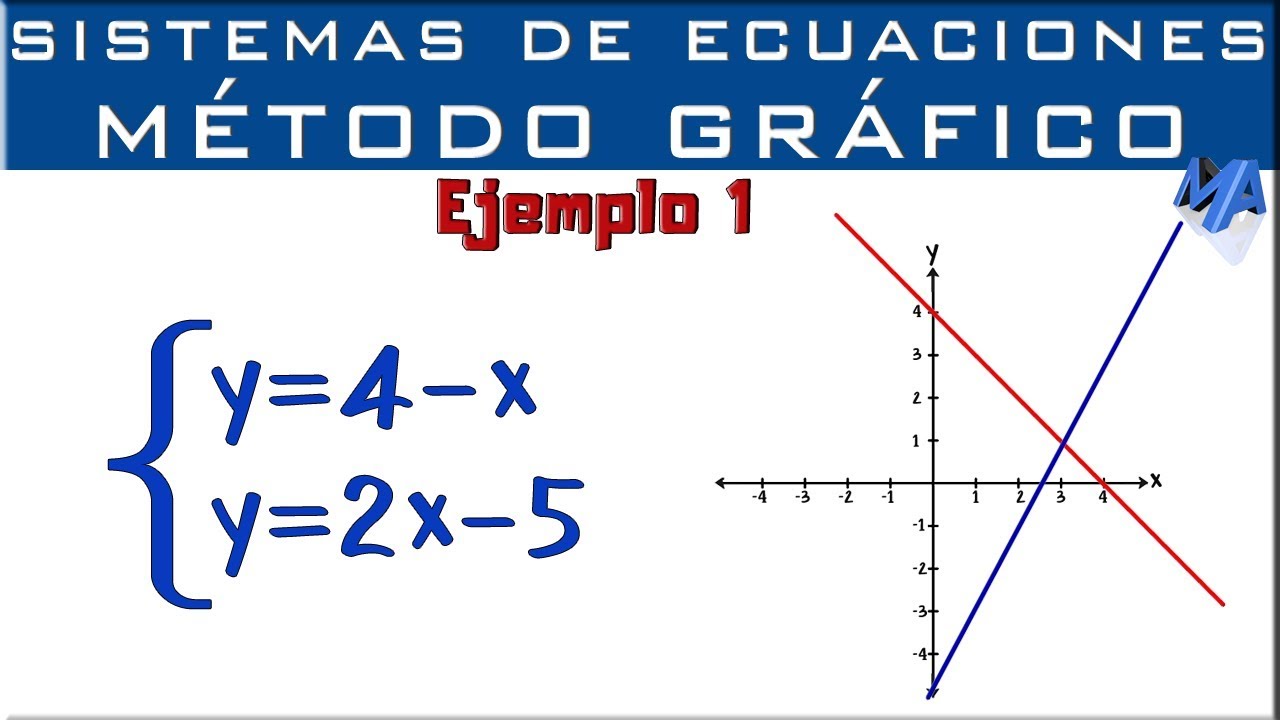
Gráfica
Se procede a graficar las rectas en el plano cartesiano utilizando los puntos obtenidos en las tablas de valores. Cada par de valores (x, y) representa un punto en el plano. Se explica que si los tres puntos trazados están en línea recta, es probable que los cálculos sean correctos. Si los puntos no forman una línea recta, se recomienda revisar los cálculos en la tabla de valores. Una vez trazadas ambas rectas, la solución del sistema de ecuaciones es el punto donde se cruzan. En este caso, el punto de intersección es (3, 1), lo que significa que x=3 e y=1. Se aconseja verificar esta solución sustituyendo estos valores en las ecuaciones originales para confirmar que satisfacen ambas ecuaciones.
Ejercicio de práctica
Se presenta un ejercicio de práctica para que los espectadores resuelvan un sistema de ecuaciones utilizando el método gráfico. Se muestran los valores de ejemplo (0, 1 y 2) para crear la tabla y los resultados obtenidos al reemplazar estos valores en las ecuaciones. Se explica cómo ubicar los puntos en el plano cartesiano y trazar las rectas, identificando el punto de corte como la solución del sistema. En este caso, la solución es x=4 e y=7. Finalmente, se recuerda la importancia de verificar la solución reemplazando estos valores en las ecuaciones originales para asegurar su validez.