Breve Riassunto
Questo video introduce il concetto di funzione in matematica, spiegando la definizione formale, la notazione, e le diverse rappresentazioni, come diagrammi a frecce e grafici cartesiani. Vengono definiti dominio, codominio e insieme immagine, e si discute come determinare il dominio naturale di una funzione quando non è esplicitamente specificato.
- Definizione di funzione come relazione tra due insiemi.
- Introduzione a dominio, codominio e immagine di una funzione.
- Rappresentazione grafica delle funzioni nel piano cartesiano.
Cos'è una Funzione?
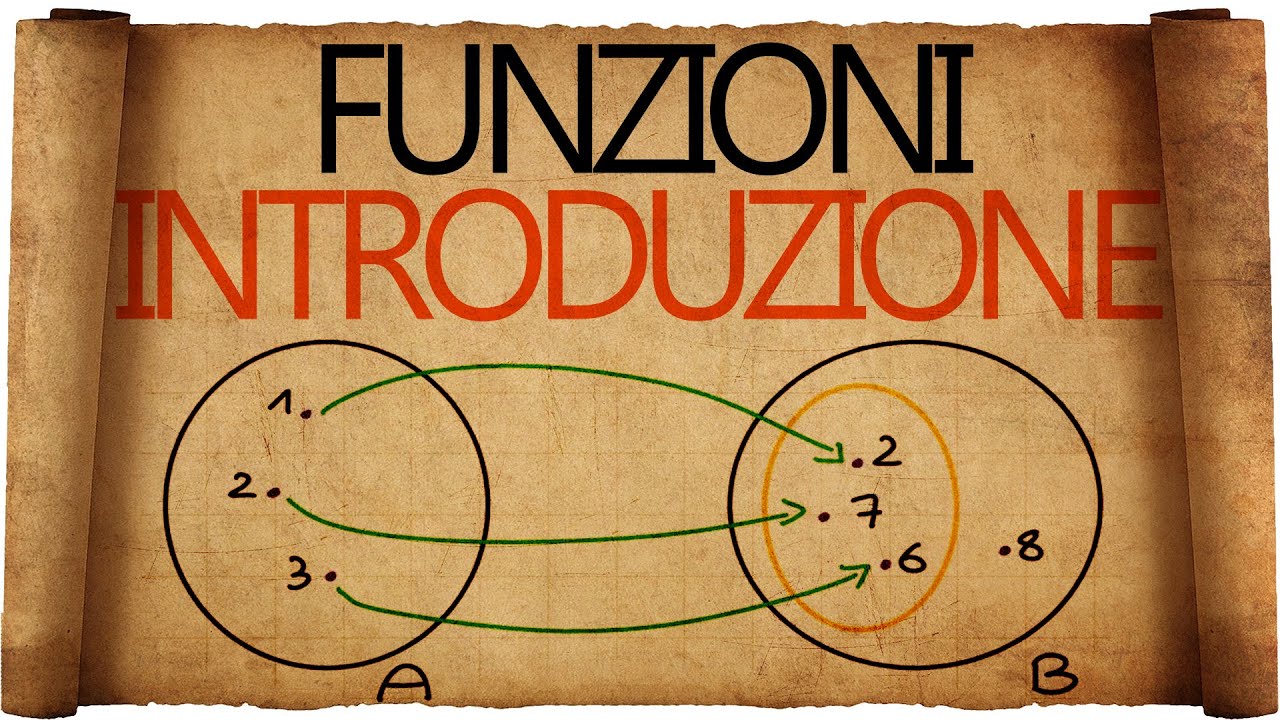
Una funzione è definita come una relazione tra due insiemi, A e B, dove ogni elemento di A è associato a un unico elemento di B. Questa associazione è spesso rappresentata con la notazione f: A → B. L'elemento b in B associato a un elemento a in A è indicato come f(a). È fondamentale che da ogni elemento di A parta una sola "freccia" verso B, ma più elementi di A possono essere associati allo stesso elemento in B, e non tutti gli elementi di B devono necessariamente essere associati a un elemento di A.
Esempi e Nomenclatura
Viene fornito un esempio numerico per illustrare come una funzione associa elementi tra due insiemi. Ad esempio, se f(1) = 2, f(2) = 7 e f(3) = 6, questo significa che la funzione f associa l'elemento 1 del dominio all'elemento 2 del codominio, e così via. Il dominio è l'insieme di partenza (A), mentre il codominio è l'insieme di arrivo (B). L'immagine di un elemento a del dominio è l'elemento f(a) nel codominio.
Insieme Immagine
L'insieme immagine di una funzione è il sottoinsieme del codominio che contiene tutti gli elementi che sono immagini di almeno un elemento del dominio. In altre parole, sono gli elementi del codominio "colpiti" da una freccia proveniente dal dominio. Se ogni elemento del codominio è l'immagine di almeno un elemento del dominio, allora l'insieme immagine coincide con l'intero codominio, e la funzione è detta suriettiva.
Rappresentazione Grafica
Quando il dominio ha molti elementi, la rappresentazione a frecce diventa impraticabile. In questi casi, si utilizza il grafico della funzione nel piano cartesiano. L'asse x rappresenta il dominio, e l'asse y rappresenta il codominio. Un punto (x, y) sul grafico indica che f(x) = y. Il grafico permette di visualizzare facilmente le proprietà della funzione.
Esempi di Grafici e Domini Naturali
Vengono mostrati esempi di grafici di funzioni come f(x) = √x e f(x) = 2^x. Si spiega come determinare il dominio e l'insieme immagine dal grafico. Quando il dominio e il codominio non sono esplicitamente specificati per una funzione definita da un'espressione matematica, si assume che il dominio sia il più grande sottoinsieme dei numeri reali in cui l'espressione ha significato (dominio naturale), e il codominio sia l'insieme dei numeri reali. Ad esempio, per f(x) = log₂(x), il dominio naturale è l'insieme dei numeri reali positivi.