Breve Sommario
Questo video analizza il moto del proiettile con un angolo di lancio diverso da zero, dimostrando che la traiettoria è parabolica. Si basa sul principio di indipendenza dei moti, combinando un moto orizzontale rettilineo uniforme e un moto verticale uniformemente accelerato. Vengono esaminate le condizioni iniziali, le leggi del moto e l'equazione cartesiana della traiettoria, per poi ricavare l'altezza massima e la gittata. Infine, si discute l'angolo ottimale di lancio e l'effetto dell'attrito sulla traiettoria.
- Principio di indipendenza dei moti
- Traiettoria parabolica
- Angolo di lancio ottimale: 45 gradi
- Effetto dell'attrito sulla traiettoria
Introduzione al Moto Parabolico
Il video introduce il concetto di moto del proiettile con un angolo di lancio, un argomento più complesso rispetto al lancio orizzontale trattato nel video precedente. Si anticipa che verrà dimostrato come la traiettoria del proiettile sia una parabola. Viene consigliato di visionare il video precedente per chi si avvicina per la prima volta a questo argomento.
Principio di Indipendenza dei Moti
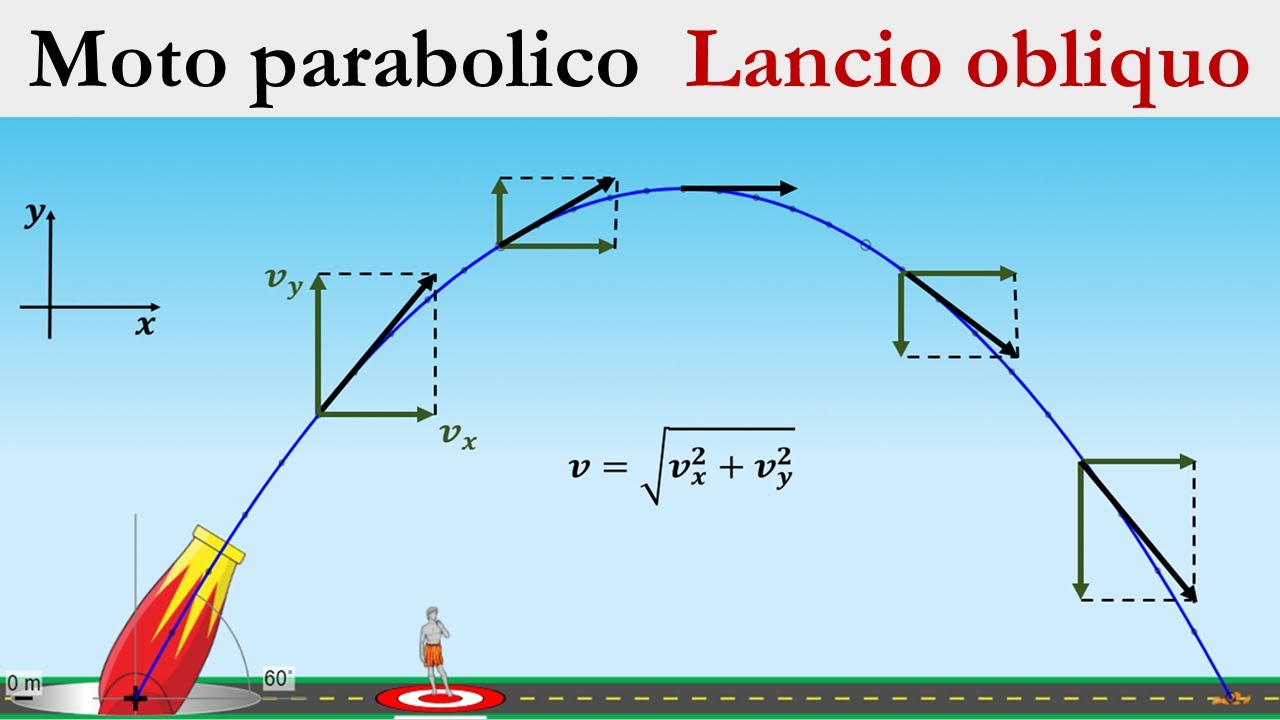
Viene ribadito il principio di indipendenza dei moti, fondamentale per comprendere il moto parabolico. Questo principio afferma che un corpo soggetto a due movimenti contemporaneamente è regolato dalle stesse leggi che si applicano quando ogni movimento avviene singolarmente. Nel caso del moto del proiettile, si combinano un moto orizzontale rettilineo uniforme (velocità costante) e un moto verticale uniformemente accelerato.
Analisi di Accelerazione, Velocità e Spostamento
Si analizzano accelerazione, velocità e spostamento del proiettile lungo la traiettoria. L'accelerazione è costante, rivolta verso il basso e pari a -g (accelerazione di gravità). La velocità è sempre tangenziale alla traiettoria e può essere scomposta in due componenti: la componente orizzontale (x) è costante, mentre la componente verticale (y) diminuisce in salita, si annulla nel punto più alto e aumenta in discesa. La velocità totale si calcola con il teorema di Pitagora.
Condizioni Iniziali e Angolo di Lancio
Si introducono le condizioni iniziali, definendo l'angolo di lancio (α) come l'angolo tra il cannone e l'asse x. La velocità iniziale lungo l'asse x (v₀ₓ) è uguale alla velocità iniziale per il coseno di α, mentre la velocità iniziale lungo l'asse y (v₀y) è uguale alla velocità iniziale per il seno di α.
Leggi del Moto
Vengono presentate le leggi del moto: l'accelerazione orizzontale è zero, mentre quella verticale è -g. La velocità orizzontale è costante e pari alla velocità iniziale orizzontale. La velocità verticale segue la formula del moto uniformemente accelerato: v_y = v₀y - gt. Le leggi orarie descrivono la posizione in funzione del tempo: x = v₀ₓt e y = -½gt² + v₀yt.
Equazione Cartesiana della Traiettoria
Si ricava l'equazione cartesiana della traiettoria, che esprime y in funzione di x. Questo si ottiene esplicitando il tempo dalla prima equazione (x = v₀ₓt) e sostituendolo nella seconda equazione (y = -½gt² + v₀yt). Il risultato è un'equazione del tipo y = ax² + bx, che conferma che la traiettoria è una parabola.
Altezza Massima e Gittata
Si spiega come ricavare l'altezza massima e la gittata dalla equazione cartesiana della traiettoria. Si suggerisce di utilizzare le formule del vertice della parabola, dove l'ascissa del vertice rappresenta metà della gittata e l'ordinata rappresenta l'altezza massima. Vengono fornite le formule per calcolare l'ascissa e l'ordinata del vertice in termini di velocità iniziali e accelerazione di gravità.
Angolo Ottimale di Lancio
Si discute l'angolo ottimale di lancio per massimizzare la gittata. Intuitivamente, un angolo troppo piccolo favorisce la velocità orizzontale ma fa cadere l'oggetto rapidamente, mentre un angolo troppo grande aumenta l'altezza ma riduce la distanza percorsa. Si dimostra algebricamente che l'angolo ottimale è di 45 gradi, utilizzando formule trigonometriche e la proprietà che il seno di 90 gradi è massimo (pari a 1).
Simulazione e Verifica dell'Angolo Ottimale
Viene presentata una simulazione per verificare l'angolo ottimale di lancio. Si confrontano gittate ottenute con angoli diversi, confermando che 45 gradi produce la gittata massima. Si osserva anche che angoli complementari (ad esempio, 35 e 55 gradi) producono la stessa gittata.
Effetto dell'Attrito
Si analizza l'effetto dell'attrito sulla traiettoria. In una situazione reale, l'attrito con l'aria deforma la parabola, rendendola asimmetrica e riducendo la gittata. L'effetto dell'attrito dipende dall'oggetto lanciato: oggetti aerodinamici come le palline da golf risentono meno dell'attrito rispetto a oggetti meno aerodinamici come le zucche. La palla di cannone, grazie alla sua massa elevata, mantiene una traiettoria simile a quella ideale anche in presenza di attrito.
Conclusioni
Si conclude anticipando un terzo video dedicato alla risoluzione di problemi sul moto parabolico. Si ribadisce l'importanza del principio di indipendenza dei moti per la comprensione e la risoluzione di problemi relativi al moto parabolico.